Rotational Mechanics : Moment of Inertia

Learning how to calculate Moment of Inertia is the first step to studying Rotational Mechanics. And calculating Moment of Inertia is a bit tricky, you may be considering the wrong dM or performing some logical or calculating error. This post is going to Involve some Basic Integration. That is the only prerequisite.

---

Rotational Mechanics and Linear setups have a lot in common. Every formula that you have studied before has a corresponding Formula for rotation. Moment of Inertia is equivalent to Mass in a linear setup. Torque is equivalent to force and displacement, velocity, acceleration and momentum are replaced by angular displacement, angular velocity, angular acceleration and angular momentum. And Every formula remains the same in basically, just replace Force with Torque, mass with Moment of Inertia.... ( get the point right ? ). More of those discussions later. Lets move on to Moment of Inertia ( Symbol : I )

There is only one basic formula, I = Mr² . Here M is the mass of the object which is at a distance r from the axis of rotation. Always remember, angular quantities are calculated about the axis of rotation.

The above formula can be used only in some cases. Suppose we have two point masses M₁ and M₂ at distances r₁ and r₂ from the axis of Rotation. Then the Moment of Inertia of this two particle system = M₁ r₁ ² + M₂ r₂ ² . However in case of a circular disc rotating about it's center, like a CD , we cannot apply the formula directly because each part of the disc is not at the same distance from the axis of rotation.

---

Moment of Inertia of a Rod

 Consider a Rod of Mass M, Length L which has it's Center of Mass at the origin and lies along the X-axis. What will be it's moment of inertia about the x-axis?

The radius is negligible compared to the length

If we assume the rod to be very thin ( negligible radius ) then about the x-axis it has zero moment of Inertia. The distance from the axis of rotation is zero and hence the Moment of Inertia is also zero.

If you were asked to find it's moment of Inertia about the y-axis then you would have to integrate.

To figure the Moment of Inertia in this case consider a small mass dm which is at a distance r from the axis of rotation. The mass dm =  Mass per unit length of the rod * dr = Mdr/L. The Moment of Inertia of this small Mass is dm.r² = (Mr² dr)/L Now all you need to do is Integrate this expression from -L/2 to L/2 ( Since the center is assumed at the origin ).

Extending this same logic forward how would you determine the Moment of Inertia in this case ?

We can follow a process similar to the previous one. Only this time the origin is at one end so the Limits of  Integration will change. Integrate the expression we had last time from 0 to L and you will get your answer. Alternatively you can apply the Parallel Axis theorem. If you know an object's Moment of Inertia about an axis passing through its Center of Mass, then it's Moment of Inertia about any axis parallel to this axis and at a distance x from it is given by I_{Center of Mass} + Mx² .

Applying it in this case we get, I_total = I_{Center of Mass} + M(L/2)² .

---

Moment of Inertia of Circular Objects

There are four standard objects and you need to remember the Moments of Inertia of each of these. I won't be giving you the answers here :-P, but I will tell you how to get your answers yourself. We'll start with the simplest, a Ring.

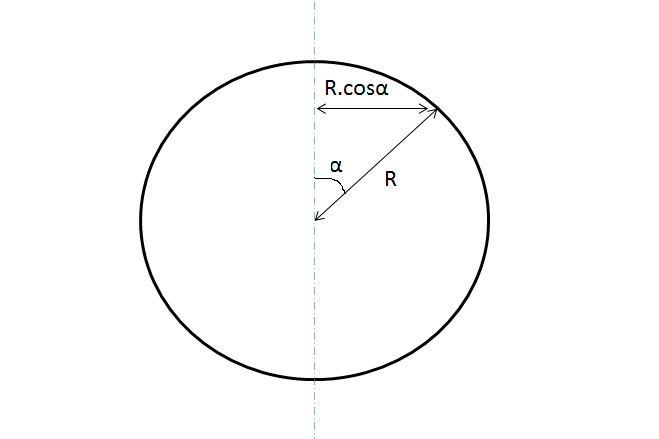
To calculate the Moment of Inertia about the Z-axis we can use the simple formula I=Mr² since every small mass dm of the ring is at the same distance r from the z-axis. To calculate the Moment of Inertia about the other axes we need to use the Perpendicular Axis Theorem.

The statement of this theorem is : I_z = I_x + I_y .For this ring I_x = I_y because they are both symmetrical, infact the moment of Inertia will be the same about any axis in the x-y plane and passing through the center of the ring. So utilizing the Perpendicular Axis formula you will obtain that I_x = MR² /2.

Note: The Perpendicular Axis Theorem is not valid for 3-D objects. The moment of Inertia of a Sphere or Cube is the same along all three axes.

Next we move on to a disc. Assume that the disc is placed similar to the ring. We can consider the disc to be made up of multiple rings of mass dm. Consider a ring of width dr at a distance r from the center. The Mass of this segment = Mass per unit area of disc * Area of segment . The area of segment will be 2πr.dr. Therefore Mass = M.(2πrdr)/πR² . Now multiply this with r² and Integrate from 0 to R ( R : Radius of disc , r : Radius of Segment ).

Tip: To Check if you have calculated mass of segment correctly, integrate it over the range of the object. You should thus get M ( The mass of the object ).

As we saw here, we can consider a Disc to be made up of rings to calculate it's moment of inertia. Similarly we can Consider a hollow Sphere to be made up of multiple rings and Thus Calculate it's Moment of Inertia. Suppose this is the cross-section of a hollow sphere.

The disc we are considering is at a distance R.cosα from the axis of Rotation. The Mass of the disc = Total Mass of Sphere * Area of the segment ( 2πRcosα . Rdα ) / Area of the Sphere ( 4πr² ). Now multiply the Mass with (R.cosα)² and Integrate from 0 to π . If you want to calculate the Moment of Inertia of a Solid Sphere, Break it up into multiple Hollow Spheres.

---

Check Your Understanding

If you already knew about Moment of Inertia before reading this post, continue ahead. If you did not know about it, and this post was your Introduction to this topic, go back and do all the Math I've mentioned. Pure reading won't be of much use.

Ready to apply what you've learnt? Think about tight-rope walkers. How does that long rod help them?

Scroll down and Comment your answers. Also, an Interesting experiment for first-timers, roll different objects of the same mass down an Inclined Plane. You will notice that despite having the same mass each takes different amount of Time.

Feel free to Comment. Also if you know of any other Interesting applications of Moment of Inertia, It would be awesome if you could share them,

Remember : Moment of Inertia is equivalent to Mass.

Picture Credits :

Rod rotating about axis By Krishnavedala (Own work) [CC0], via Wikimedia Commons

Ring rotating with labelled axes By Grendelkhan at the English language Wikipedia [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/)], via Wikimedia Commons
Man crossing Niagara Falls By George Barker [Public domain], via Wikimedia Commons
All other pictures by © MridulKothari